##이진탐색트리_삭제_메소드_이론 :




##이진탐색트리_삭제_메소드_비재귀,삭제_이론 + 코드 :

##이진탐색트리_삭제_메소드_재귀,삭제_이론 + 코드 :





##자주 햇갈리는 개념 :
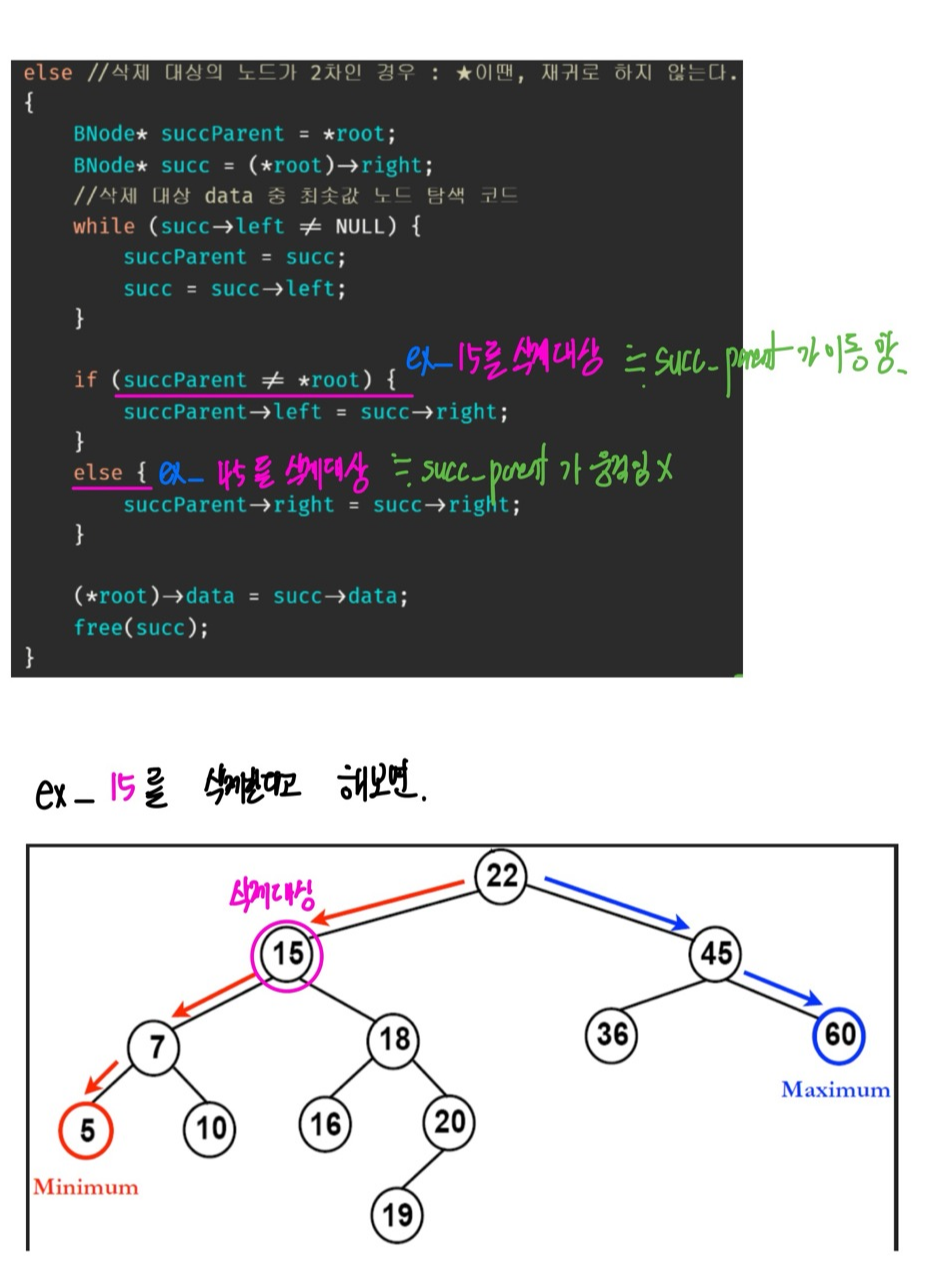
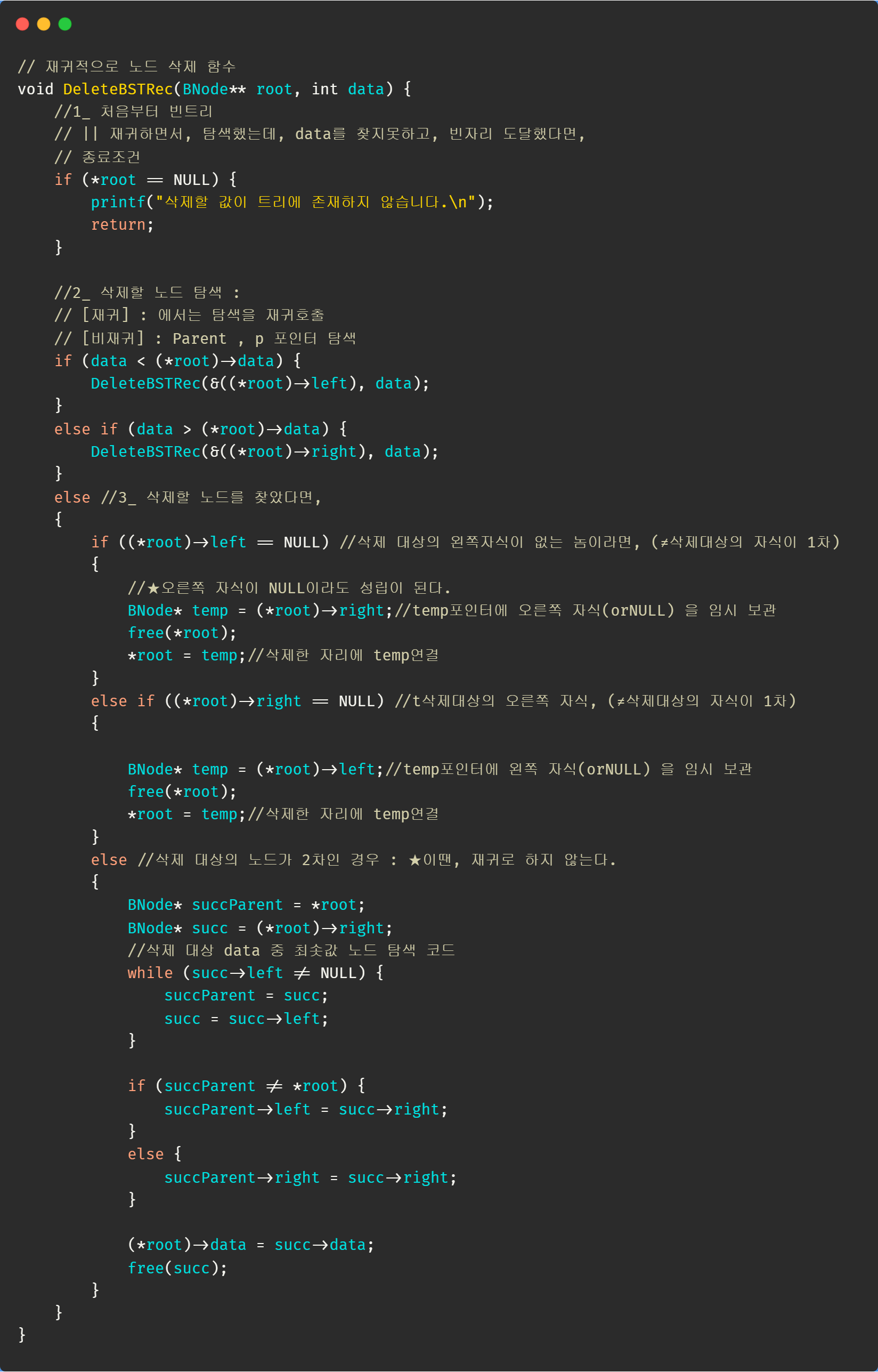
★삭제 대상 노드의 자식이 2명인 경우 :
1_ succ_parent 자손 지정
- succ_parent가 움직였을 경우 => succ_parent의 왼쪽자손을 succ의 오른쪽자손으로 업데이트
- succ_parent가 움직이지 않았을 경우 => succ_parent의 오른쪽 자손을 succ의 오른쪽자손으로 업데이트
2_ 다른 Case와 다르게 삭제 대상 노드의 자식이 2명인 경우는 *root노드를 지우는 것이 아닌 succ노드를 지우는 것
##전체 코드 :
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
|
#include <stdio.h>
#include <stdlib.h>
#pragma warning (disable : 4996)
// 이진트리 구조체
typedef struct _BSTNode {
struct _BSTNode* left;
struct _BSTNode* right;
int data;
} BNode;
// 탐색 : 재귀
BNode* SearchBST(BNode* root, int data) {
// 종료조건
if (root == NULL) {
printf("%d은 이진트리탐색에 존재하지 않습니다.\n", data);
return root;
}
if (root->data > data) {
// 왼쪽 재귀
return SearchBST(root->left, data);
}
else if (root->data < data) {
// 오른쪽 재귀
return SearchBST(root->right, data);
}
else return root;
}
// 삽입 : 재귀
void InsertBST(BNode** root, int data) {
// ★삽입 메소드는 재귀지만, 종료조건이 없음
// 1_ 빈트리에 삽입한다면,
if (*root == NULL) {
*root = (BNode*)malloc(sizeof(BNode));
(*root)->data = data;
(*root)->left = NULL;
(*root)->right = NULL;
return;
}
// 2_ 빈트리가 아니리면, 탐색(data가 들어갈 자리) , 빈자리시 삽입
if ((*root)->data > data) { // 왼쪽으로 탐색
InsertBST(&((*root)->left), data);
}
else if ((*root)->data < data) { // 오른쪽으로 탐색
InsertBST(&((*root)->right), data);
}
else {
printf("%d가 이미 트리안에 중복값으로 존재합니다.\n", data);
return;
}
}
// 재귀적으로 노드 삭제 함수
void DeleteBSTRec(BNode** root, int data) {
if (*root == NULL) {
printf("삭제할 값이 트리에 존재하지 않습니다.\n");
return;
}
if (data < (*root)->data) {
DeleteBSTRec(&((*root)->left), data);
}
else if (data > (*root)->data) {
DeleteBSTRec(&((*root)->right), data);
}
else {
if ((*root)->left == NULL) {
BNode* temp = (*root)->right;
free(*root);
*root = temp;
}
else if ((*root)->right == NULL) {
BNode* temp = (*root)->left;
free(*root);
*root = temp;
}
else {
BNode* succParent = *root;
BNode* succ = (*root)->right;
while (succ->left != NULL) {
succParent = succ;
succ = succ->left;
}
if (succParent != *root) {
succParent->left = succ->right;
}
else {
succParent->right = succ->right;
}
(*root)->data = succ->data;
free(succ);
}
}
}
// 이진 탐색 트리 출력 (중위 순회 하면, 오름차순 출력)
void InOrder(BNode* root) {
if (root == NULL) return;
// L
if (root->left != NULL) InOrder(root->left);
// D
printf(" %d", root->data);
// R
if (root->right != NULL) InOrder(root->right);
}
int main() {
BNode* Tree1 = NULL;
InsertBST(&Tree1, 23);
InsertBST(&Tree1, 11);
InsertBST(&Tree1, 1);
InsertBST(&Tree1, 139);
InsertBST(&Tree1, 67);
InOrder(Tree1);
printf("\n");
DeleteBSTRec(&Tree1, 23);
DeleteBSTRec(&Tree1, 11);
DeleteBSTRec(&Tree1, 9);
InOrder(Tree1);
printf("\n");
return 0;
}
|
cs |
##출력 화면 :

'알고리즘(C언어) > 이것이 자료구조+알고리즘이다(박상현)_자료구조' 카테고리의 다른 글
| (15)[Chapter6]AVL 트리_삭제 메소드(작성중) (0) | 2024.08.04 |
|---|---|
| (14)[Chapter6]AVL 트리_삽입 메소드 (0) | 2024.08.03 |
| (12)[Chapter6]이진 탐색 트리_탐색,삽입메소드(이론 + 코드) (3) | 2024.07.23 |
| (11)[Chapter6]이진 탐색(이론 + 코드) (0) | 2024.07.21 |
| (10)[Chapter6]순차탐색_계수법(이론+코드)(작성중) (0) | 2024.07.19 |
