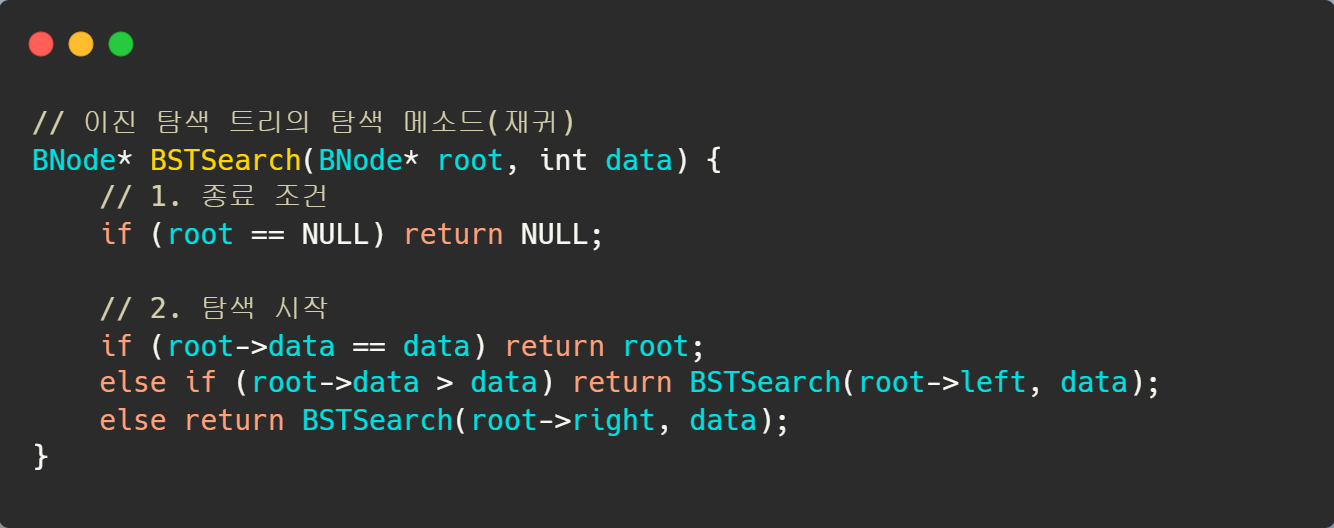
##이진 탐색 트리_Search()
##이진 탐색 트리_Insert() (비재귀)

##이진 탐색 트리_Insert() (재귀) :
- ★삽입 재귀버전은 재귀인데도, 종료조건이 따로 없다 (굳이 있다면, 저 빈트리일때가 종료조건임)
- 논리 순서 :
1_ 빈트리라면 : "if(*root==NULL)",
2_ data가 들어갈 자리를 탐색 하면서, 재귀 호출 :

##이진 탐색 트리_오름차순 출력 => 중위 순회

##전체 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
|
#include <stdio.h>
#include <stdlib.h>
#pragma warning (disable : 4996)
typedef struct _BSTNode {
int data;
struct _BSTNode* left;
struct _BSTNode* right;
} BNode;
// 이진 탐색 트리의 탐색 메소드(재귀)
BNode* BSTSearch(BNode* root, int data) {
// 1. 종료 조건
if (root == NULL) return NULL;
// 2. 탐색 시작
if (root->data == data) return root;
else if (root->data > data) return BSTSearch(root->left, data);
else return BSTSearch(root->right, data);
}
// 이진 탐색 트리 삽입 메소드 (비재귀 + 이중 포인터)
void BSTInsert(BNode** root, int data) {
// 1. 빈 트리라면,
if (*root == NULL) {
*root = (BNode*)malloc(sizeof(BNode));
(*root)->data = data;
(*root)->left = NULL;
(*root)->right = NULL;
return;
}
// 2. 빈 트리가 아니라면,
BNode* P = *root;
BNode* C = NULL;
while (P != NULL) {
// 발자취 남기기
C = P;
if (P->data > data) // 왼쪽으로 포인터 이동
{
P = P->left;
}
else if (P->data < data) {
P = P->right;
}
else {
printf("%d는 이미 트리에 중복된 값\n", data);
return;
}
}
// newNode 할당
BNode* newNode = (BNode*)malloc(sizeof(BNode));
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
if (C->data > data) {
C->left = newNode;
}
else {
C->right = newNode;
}
return;
}
// 이진 탐색 트리 삽입 메소드 (재귀)
void BSTInsertRecursive(BNode** root, int data) {
// 1. 현재 노드가 NULL이면 새로운 노드를 생성하여 삽입
if (*root == NULL) {
*root = (BNode*)malloc(sizeof(BNode));
(*root)->data = data;
(*root)->left = NULL;
(*root)->right = NULL;
return;
}
// 2. 현재 노드의 값과 비교하여 왼쪽 또는 오른쪽으로 재귀 호출
if ((*root)->data > data)
{
BSTInsertRecursive(&((*root)->left), data);
}
else if ((*root)->data < data)
{
BSTInsertRecursive(&((*root)->right), data);
}
else
{
printf("%d는 이미 트리에 중복된 값\n", data);
return;
}
}
// 이진 탐색 트리 출력 (중위 순회 하면, 오름차순 출력)
void InOrder(BNode* root) {
if (root == NULL) return;
// L
if (root->left != NULL) InOrder(root->left);
// D
printf(" %d", root->data);
// R
if (root->right != NULL) InOrder(root->right);
}
int main() {
BNode* Tree1 = NULL;
BSTInsert(&Tree1, 23);
BSTInsert(&Tree1, 11);
BSTInsert(&Tree1, 1);
BSTInsert(&Tree1, 139);
BSTInsert(&Tree1, 67);
InOrder(Tree1);
printf("\n");
return 0;
}
|
cs |
'알고리즘(C언어) > 이것이 자료구조+알고리즘이다(박상현)_자료구조' 카테고리의 다른 글
| (14)[Chapter6]AVL 트리_삽입 메소드 (0) | 2024.08.03 |
|---|---|
| (13)[Chapter6]이진 탐색 트리_삭제 메소드_비재귀/재귀(이론 + 코드) (5) | 2024.07.25 |
| (11)[Chapter6]이진 탐색(이론 + 코드) (0) | 2024.07.21 |
| (10)[Chapter6]순차탐색_계수법(이론+코드)(작성중) (0) | 2024.07.19 |
| (10)[Chapter6]순차탐색_전진이동법,전위법(코드편) (작성중) (0) | 2024.07.19 |

